რამდენად გახსოვთ სკოლაში ნასწავლი მათემატიკა? შეძლებთ დაეხმაროთ ბავშვებს დავალებების ამოხსნაში?
დღეს ჩვენ გთავაზობთ 2 ძალიან განსხვავებულ, მაგრამ საინტერესო ამოცანებს. მათი ამოხსნა შეუძლია ყველას, ვინც მათემატიკასთან მეგობრობს. გამოსცადე შენი გონება – არის თუ არა ის ტონუსში და რამდენად გაუმკლავდება ის ამ ამოცანებს.
მათემატიკური მაგალითები
1. ეს ერთი შეხედვით მარტივი მათემატიკური მაგალითია, მაგრამ სხვადასხვა ადამიანი სხვადასხვა პასუხს იღებს.
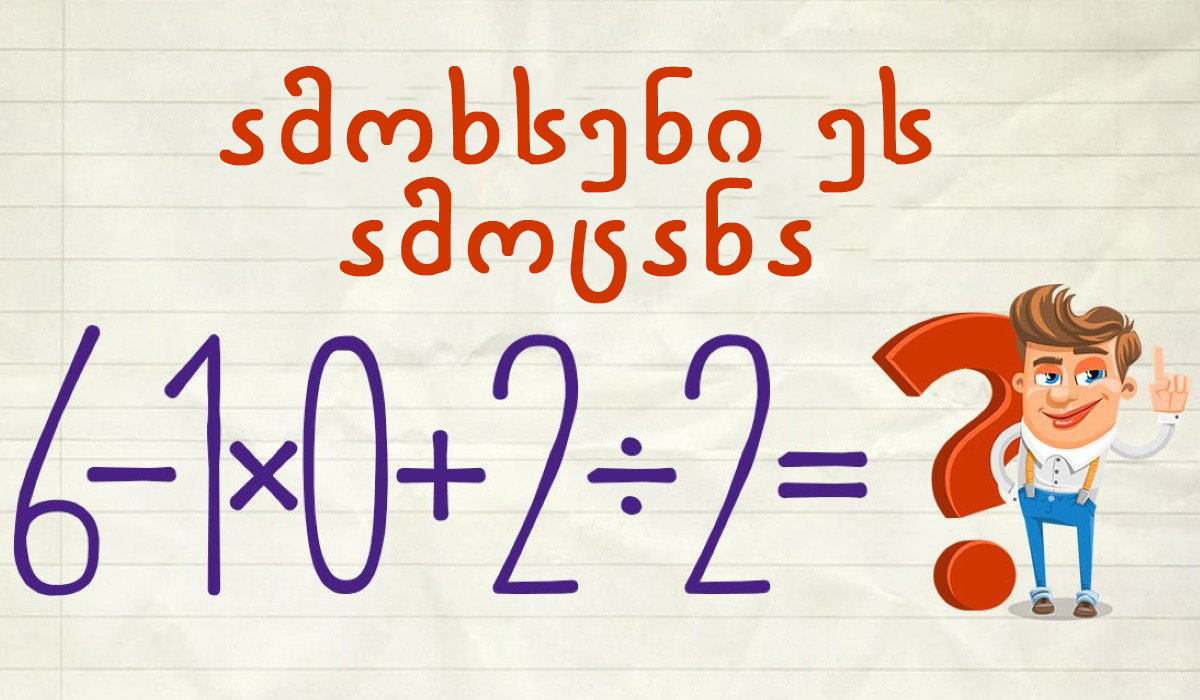
2. თუ ზედა მაგალითს თავი ადვილად გაართვით, ახლა გთავაზობთ ლოგიკურ ამოცანას.
თქმულების თანახმად, სულთანმა რაინდი დაატყვევა. გათავისუფლება იმ პირობით შესთავაზა, თუ მარტივ ამოცანას ამოხსნიდა.
ამოცანა ასეთია: ,,შენ მოგცემენ 12 ერთმანეთის მსგავს მონეტას და სასწორს გირების გარეშე. ერთ-ერთი მონეტა ყალბია. თუმცა არავინ იცის, ის სხვებზე მძიმეა თუ მსუბუქი. გეძლევა 3 აწონვის შანსი ყალბი მონეტის აღმოსაჩენად.”
როგორ უნდა იპოვო 12 მონეტაში ყალბი 3 აწონვით და შესაძლებელია თუ არა ამის ამოხსნა?
პასუხები
1. მაგალითის ამოსახსნელად გაიხსენე, რომ ჯერ სრულდება გამრავლება და გაყოფა, შემდეგ კი მიმატება და გამოკლება.
მაგალითი მიიღებს ამ სახეს: 6 – 1 * 0 + 2 / 2 = 6 – 0 + 1 = 7.
2. მეორე ამოცანას დიდი დრო სჭირდება. ყველაზე რთული ისაა, რომ არ ვიცით ყალბი მონეტა დანარჩენებზე მძიმეა თუ მსუბუქი.
პირველ რიგში, მონეტები გავყოთ 3 ტოლ ნაწილად. ავწონოთ მონეტების პირველი 2 პარტია. თუ ისინი თანაბარი წონისაა, ესე იგი, ყალბი მონეტა მესამე გროვაშია.
ახლა ავწონოთ ნებისმიერი 2 ნამდვილი მონეტა (პირველი და მეორე ჯგუფიდან) და 2 მონეტა ბოლო გროვიდან. თუ სასწორი კვლავ თანაბარს აჩვენებს, ესე იგი, ყალბი მონეტა დარჩენილ 2 ცალშია. ამიტომ მესამე საფეხურად ვწონით ჩვენთვის ნაცნობი ნამდვილი მონეტებიდან ერთს და დარჩენილი 2 მონეტიდან ერთ-ერთს. თუ წონა კვლავ თანაბარია, ესე იგი, ყალბ მონეტას არც შევხებივართ. თუ არათანაბარია, ესე იგი, ყალბი ამ 2-ს შორის არის.
თუ მეორე აწონვისას არათანაბრობაა, ესე იგი, ყალბი მონეტის წყვილი ნაპოვნია. არანამდვილი მონეტის პოვნა მესამე აწონვით ასევე არ წარმოადგენს სირთულეს.
თუ პირველი აწონვისას, ერთი ჯგუფი უფრო მძიმე აღმოჩნდა, ესე იგი, ყალბი მონეტა ამ პირველ რვაშია. ამ შემთხვევაში, უმჯობესი იქნება ყველა მონეტას ნომერი მივანიჭოთ: პირველი გროვა (მძიმე) – 1,2,3,4; მეორე (მსუბუქი) — 5,6,7,8; მესამე (ნამდვილი) — 9,10,11,12.
მეორე ნაბიჯად ავწონოთ 1,9,10,11 და 2,3,4,5. თუ თანაბარია, ესე იგი, ყალბი არის 6,7 ან 8. პირველი აწონვის შემდეგ უკვე გავიგეთ, რომ მეორე პარტია უფრო მსუბუქია, ესე იგი, ყალბი ორიგინალზე მსუბუქია. ამიტომ ვწონით 6-ს და 7-ს. რომელიც მსუბუქია, ის არის ყალბი. თუ თანაბარია, ესე იგი, ყალბი მონეტაა 8.
თუ მეორე ნაბიჯის შემდეგ ვნახდეთ, რომ ჯგუფი 1,9,10,11 უფრო მძიმეა, ვიდრე ჯგუფი 2,3,4,5, ესე იგი, ყალბი ან არის 1 (უფრო მძიმე) ან 5 (უფრო მსუბუქი). საკმარისია ავწონოთ, ვთქვათ, 1 ან ნებისმიერი ნამდვილი მონეტა. თუ 1 უფრო მძიმეა, ესე იგი, ყალბი ის არის. თუ თანაბარია, ყალბი 5 გამოდის.
იმ შემთხვევაში, თუ ჯგუფი 2,3,4,5 უფრო მძიმე იქნება, ეს ნიშნავს, რომ ყალბი მონეტა უფრო მძიმეა. და ის არის 2,3,4 ჯგუფში. ასეთ შემთხვევაში უნდა ავწონოთ 2 ან 3. რომელიც უფრო მძიმეა, ესე იგი, ის ყალბია. თუ ტოლია, მაშინ ყალბი აღმოჩნდება მონეტა 4.
ჰუჰ! აი ასეთი არამარტივი აღმოჩნდა ეს ბოლო ამოცანა. ვიმედოვნებთ, რომ ძალიან არ დაგაბნიეთ.
თქვენ უფრო მარტივი ხერხი ხომ არ იპოვეთ ამოსახსნელად? თუ ასეა მოგვიყევით კომენტარებში!
